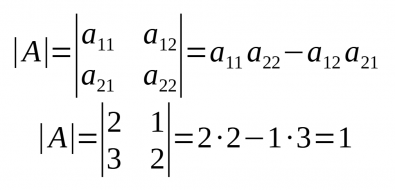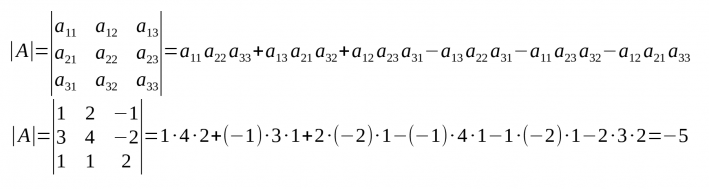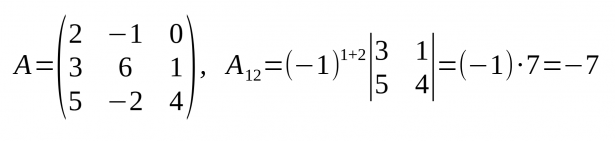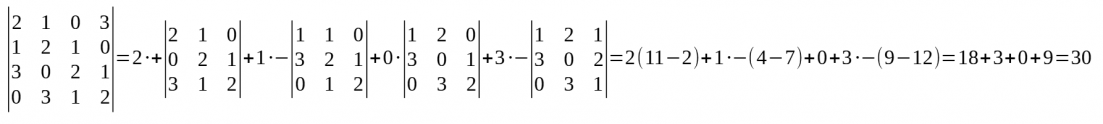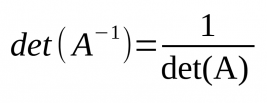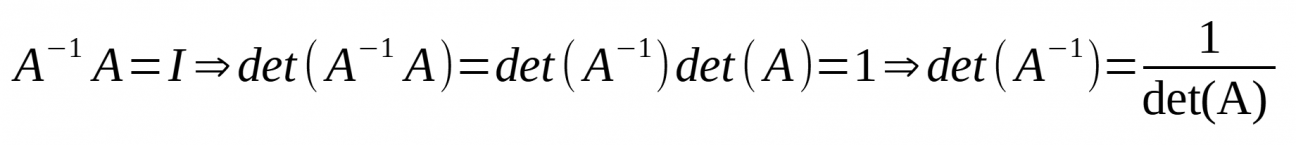Determinants

Definició

• A les matrius quadrades de nombres reals se'ls pot associar un nombre anomenat determinant.

Determinant d'ordre 2

• Per extreure el determinant (det(A) o |A|) d'una matriu quadrada d'ordre 2 s'ha de fer:

Determinant d'ordre 3

• Per extreure el determinant (det(A) o |A|) d'una matriu quadrada d'ordre 3 s'ha de fer:

• Per recordar els sumands del determinant d'ordre 3 i el signe podem fer servir la regla de Sarrus:.

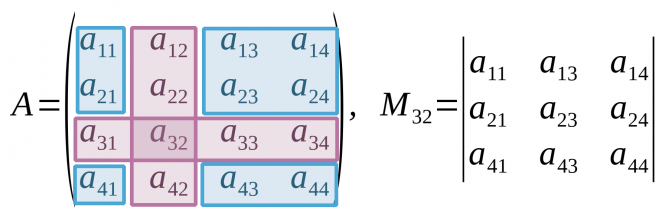
Menor d'una matriu

• El menor d'una matriu és aquell determinant que s'obté a partir del resultat d'eliminar d'una matriu quadrada qualsevol nombre de files o de columnes en una dimensió qualsevol.
• El menor complementari de l'element a_ij denotat per M_ij és aquell element que es troba en el mig de la fila i de la columna j.
• A les matrius quadrades d'ordre 2, el menor complementari de qualsevol element és un nombre.

Adjunt d'un element

• A cada menor complementari se li pot assignar un signe, positiu si és parell i negatiu si és senar.
• S'anomena de l'element a_ij (anomenat A_ij), el seu menor complementari multiplicat per (-1)^i+j:
  • (-1)^i+jM_ij

És millor pensar que d'esquerra a dreta és: + - + - i així fins a acabar la matriu que fer la formula.

Determinant d'una matriu quadrada de qualsevol ordre

• Si Aⁿ = (a^i+j) és una matriu quadrada d'ordren, el seu determinant s'obté per mitjà de la suma:
  • |A| = a¹¹A¹¹ + a¹²A¹²+a¹³ + ··· + a¹ⁿA¹ⁿ
    • A = Andjunt de l'element, a = element.

Propietats dels determinants

Característiques dels elements d'una columna o fila

• det(C₁,C₂,C₃) + det(C₁,C'₂,C₃) = det(C₁,C₂ + C'₂,C₃)
• Si una fila o columna d'una matriu quadrada es multiplica per un nombre real, el determinat de la matriu queda multiplicat per aquest nombre.
  • det(C₁,C₂,KC₃) = kdet(C₁,C₂,C₃)

Combinacions lineals

• Si tots els elemntes d'una columna o fila d'una matriu quadrada són nuls, el determinant de la matriu és zero.
  • det(C₁,0,₃) = det(₁,Csub>2-Csub>2) = det(C₁,C₂,C₃) - det(C₁,C₂,C₃) = 0
• Si una matriu quadrada té dies columnes o files iguals, el seu determinant és nul.
• Si una matriu quadrada, una columna o fila és proporcional a una altra, el seu determinant és nul.
  • det(C₁,λC₂,C₃) = λdet(C₁,C₂,C₃) = 0
• Si en una matriu quadrada una columna o fila és combinació de les seves paral·leles, el seu determinant és nul.

Transformacions en les matrius

• Si en una matriu quadrada s'intercanvien entre elles dues columnes o dues files, el seu determinant canvia de signe.
• Si en una matriu quadrada se suma a una columna o una fila una combinació lineal de les seves paral·leles, el determinant no varia.
• Si es transposa una matriu quadrada, el seu determinant no varia: |A|=|A^t|.

Operacions amb matrius

• det(A·B) = det(A) · det(B)