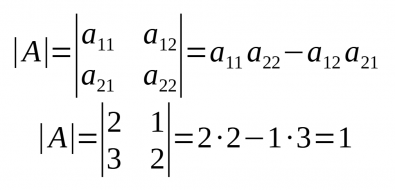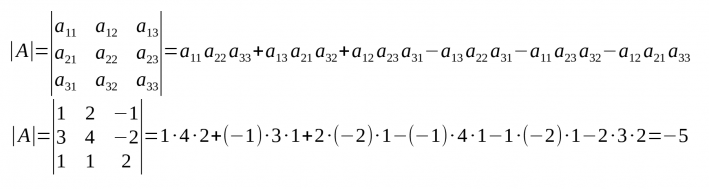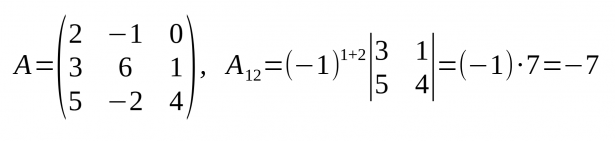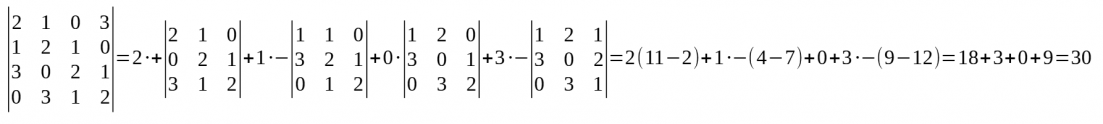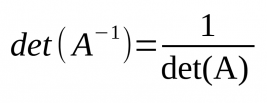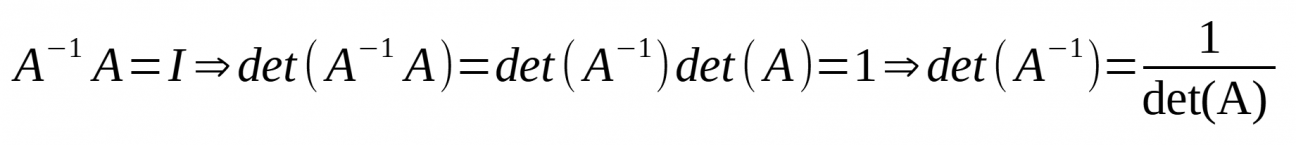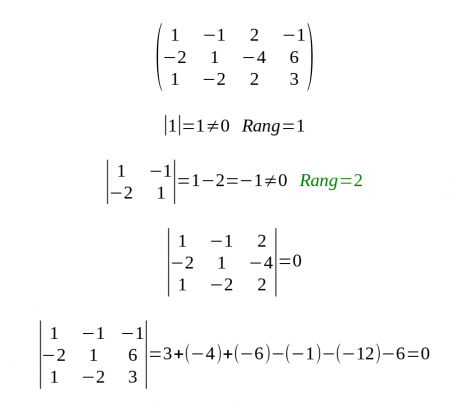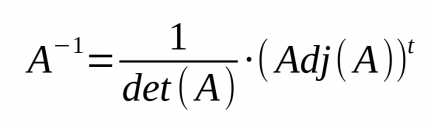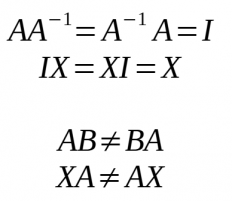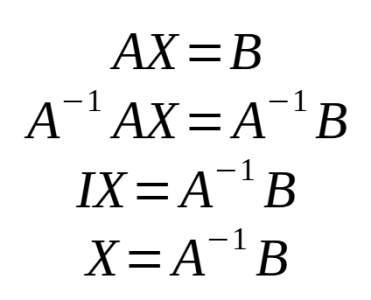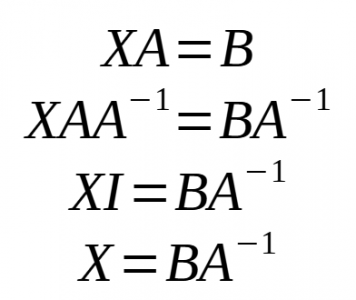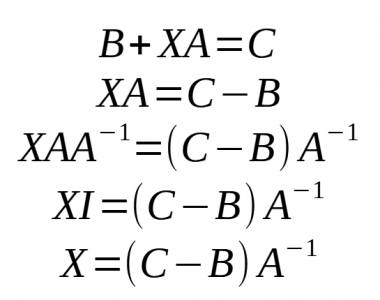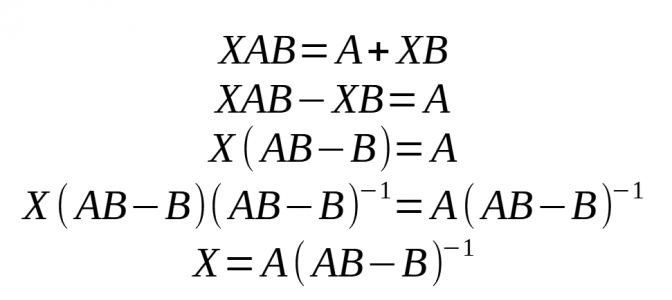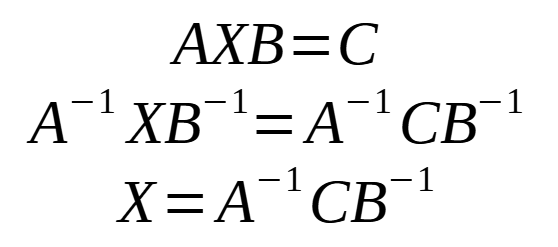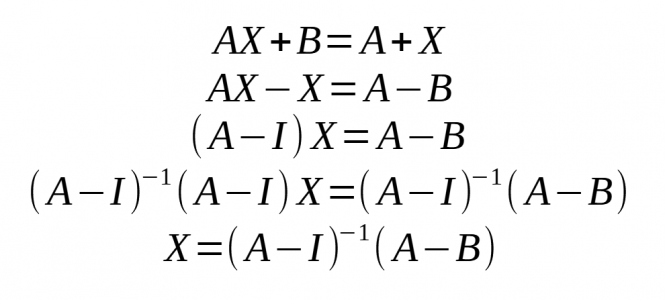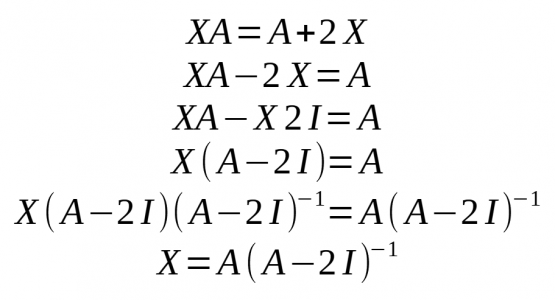Determinants: diferència entre les revisions
De FFAWiki
| (Hi ha 47 revisions intermèdies del mateix usuari que no es mostren) | |||
| Línia 18: | Línia 18: | ||
* El menor d'una matriu és aquell determinant que s'obté a partir del resultat d'eliminar d'una matriu quadrada qualsevol nombre de files o de columnes en una dimensió qualsevol. | * El menor d'una matriu és aquell determinant que s'obté a partir del resultat d'eliminar d'una matriu quadrada qualsevol nombre de files o de columnes en una dimensió qualsevol. | ||
* El '''menor complementari''' de l'element a< | * El '''menor complementari''' de l'element a<sub>ij</sub> denotat per M<sub>ij</sub> és aquell element que es troba en el mig de la fila i de la columna j. | ||
* A les matrius quadrades d'ordre 2, el '''menor complementari''' de qualsevol element és un nombre. | * A les matrius quadrades d'ordre 2, el '''menor complementari''' de qualsevol element és un nombre. | ||
: [[Fitxer:MenorsMatriu.png|cap|miniatura|672x672px]] | |||
==Adjunt d'un element== | |||
* A cada [[#Menor d'una matriu | '''menor complementari''' ]] se li pot assignar un signe, positiu si és parell i negatiu si és senar. | |||
* S'anomena de l'element a<sub>ij</sub> (anomenat A<sub>ij</sub>), el seu menor complementari multiplicat per (-1)<sup>i+j</sup>: | |||
** '''(-1)<sup>i+j</sup>M<sub>ij</sub>''' | |||
: [[Fitxer:Adjunt.png|cap|miniatura|615x615px|És millor pensar que d'esquerra a dreta és: + - + - i així fins a acabar la matriu que fer la formula.]] | |||
==Determinant d'una matriu quadrada de qualsevol ordre== | |||
* Si A<sup>n</sup> = (a<sup>i+j</sup>) és una matriu quadrada d'ordren, el seu determinant s'obté per mitjà de la suma: | |||
** '''|A| = a<sup>11</sup>A<sup>11</sup> + a<sup>12</sup>A<sup>12</sup>+a<sup>13</sup> + ··· + a<sup>1n</sup>A<sup>1n</sup>''' | |||
***'''A = Andjunt de l'element, a = element'''. | |||
: [[Fitxer:DeterminantDeQualsevolMatriuQuadrada.png|cap|miniatura|1103x1103px]] | |||
==Propietats dels determinants== | |||
===Característiques dels elements d'una columna o fila=== | |||
* '''det(C<sub>1</sub>,C<sub>2</sub>,C<sub>3</sub>) + det(C<sub>1</sub>,C'<sub>2</sub>,C<sub>3</sub>) = det(C<sub>1</sub>,C<sub>2</sub> + C'<sub>2</sub>,C<sub>3</sub>)''' | |||
* Si una fila o columna d'una matriu quadrada es multiplica per un nombre real, el determinat de la matriu queda multiplicat per aquest nombre. | |||
** '''det(C<sub>1</sub>,C<sub>2</sub>,KC<sub>3</sub>) = kdet(C<sub>1</sub>,C<sub>2</sub>,C<sub>3</sub>)''' | |||
===Combinacions lineals=== | |||
* Si tots els elemntes d'una columna o fila d'una matriu quadrada són nuls, el determinant de la matriu és zero. | |||
**'''det(C<sub>1</sub>,0,<sub>3</sub>) = det(<sub>1</sub>,Csub>2-Csub>2) = det(C<sub>1</sub>,C<sub>2</sub>,C<sub>3</sub>) - det(C<sub>1</sub>,C<sub>2</sub>,C<sub>3</sub>) = 0''' | |||
* Si una matriu quadrada té dies columnes o files iguals, el seu determinant és nul. | |||
* Si una matriu quadrada, una columna o fila és proporcional a una altra, el seu determinant és nul. | |||
** '''det(C<sub>1</sub>,λC<sub>2</sub>,C<sub>3</sub>) = λdet(C<sub>1</sub>,C<sub>2</sub>,C<sub>3</sub>) = 0''' | |||
* Si en una matriu quadrada una columna o fila és combinació de les seves paral·leles, el seu determinant és nul. | |||
** | |||
===Transformacions en les matrius=== | |||
* Si en una matriu quadrada s'intercanvien entre elles dues columnes o dues files, el seu determinant canvia de signe. | |||
* Si en una matriu quadrada se suma a una columna o una fila una combinació lineal de les seves paral·leles, el determinant no varia. | |||
* Si es transposa una matriu quadrada, el seu determinant no varia: |A|=|A<sup>t</sup>|. | |||
===Operacions amb matrius=== | |||
* '''det(A·B) = det(A) · det(B)''' | |||
* [[Fitxer:OperacionsAmbMatrius11.png|cap|miniatura|267x267px]], que aquesta relació s'obté de: | |||
** [[Fitxer:OperacionsAmbMatrius11 2.png|cap|miniatura|1296x1296px]] | |||
==Determinant d'una matriu triangular== | |||
* El determinant d'una [[Matrius#Classificaci.C3.B3_de_matrius_quadrades|matriu triangular]] és igual al producte dels elements de la diagonal principal. | |||
==Càlcul de determinants pel mètode de Gauss== | |||
* Es tracta que a partir de [[Matrius#Transformacions_que_conserven_el_rang|transformacions]] senzilles ([[Determinants#Transformacions_en_les_matrius#Transformacions_que_conserven_el_rang|tenint en compte que s'està calculant el determinant]]) aconseguir transformar la matriu en una matriu triangular. | |||
: [[Fitxer:CalcularDeterminantGauss.png|cap|miniatura|1624x1624px]] | |||
==Calcular el rang a partir dels menors d'una matriu== | |||
* Es tracta d'agafar els menors (de dimensió més petita a més gran) i fer el càlcul d'ells. En el cas que el determinant del menor sigui diferent de 0 s'entendrà que l'ordre (n) d'aquell menor serà el rang de la matriu, sempre que no hi hagi un menor d'ordre més gran que el seu determinant sigui diferent de 0. | |||
: [[Fitxer:RangMatriuDeterminants.png|cap|miniatura|456x456px|El rang és 2]] | |||
==Calcular la matriu inversa a partir de Determinants== | |||
* Si una matriu quadrada, amb determinant diferent de 0 ( '''det(A) ≠ 0''' ), amb aquesta fórmula pot calcular la matriu inversa: | |||
: [[Fitxer:FormulaInversaMatriuDeterminant.png|cap|miniatura|431x431px]] | |||
: [[Fitxer:InversaPerDeterminants.png|cap|miniatura|474x474px|Exemple]] | |||
==Equacions Matricials== | |||
===Regla de la suma=== | |||
* Si se suma la mateixa matriu als dos membres d'una igualtat matricial, es manté la igualtat. | |||
===Regla del producte=== | |||
* Si es multipliquen els dos membres d'una igualtat per un nombre real, es manté la igualtat. | |||
* Si es multipliquen els dos membres d'una equació matricial per una matriu, com que el producte de matriu no és commutatiu cal tenir en compte el costat pel qual es multiplica: | |||
** Si es multipliquen per l'esquerra els dos membres d'una igualtat matricial per una matriu, es manté la igualtat i el mateix si es multipliquen a la dreta els dos membres de la igualtat matricial, però mai un a l'esquerra i un a la dreta. | |||
===Extracció de factor comú=== | |||
* Les propietats associatives permeten treure factor comú en una expressió matricial sempre que el factor es repeteixi al mateix costat de cada producte. | |||
===Representació dels punts anteriors=== | |||
* Llavors tenien en compte tot el dit i que: | |||
:[[Fitxer:DeterminatsCosesATernirEnCompteEquacionsMatricials.png|cap|miniatura|232x232px]] | |||
* Podem dir que: | |||
<gallery widths="200" heights="200" mode="packed"> | |||
Fitxer:DeterminantsEquacionsMatricialsE1.png | |||
Fitxer:DeterminantsEquacionsMatricialsE2.png | |||
Fitxer:DeterminantsEquacionsMatricialsE3.png | |||
Fitxer:DeterminantsEquacionsMatricialsE4.png | |||
Fitxer:DeterminantsEquacionsMatricialsE5.png | |||
Fitxer:DeterminantsEquacionsMatricialsE6.png | |||
Fitxer:DeterminantsEquacionsMatricialsE7.png | |||
</gallery> | |||
* I en cas que no es pugui aplicar els casos anteriors, el que podem fer és substituir X per una matriu amb lletres: | |||
: [[Fitxer:DeterminantsEquacionsMatricialsE9.png|cap|miniatura|582x582px]] | |||
Revisió de 19:02, 16 gen 2022
Definició
- A les matrius quadrades de nombres reals se'ls pot associar un nombre anomenat determinant.
Determinant d'ordre 2
- Per extreure el determinant (det(A) o |A|) d'una matriu quadrada d'ordre 2 s'ha de fer:
Determinant d'ordre 3
- Per extreure el determinant (det(A) o |A|) d'una matriu quadrada d'ordre 3 s'ha de fer:
- Per recordar els sumands del determinant d'ordre 3 i el signe podem fer servir la regla de Sarrus:.
Menor d'una matriu
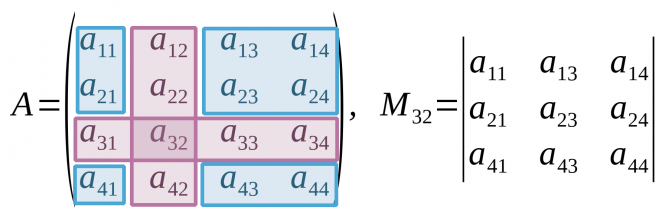
- El menor d'una matriu és aquell determinant que s'obté a partir del resultat d'eliminar d'una matriu quadrada qualsevol nombre de files o de columnes en una dimensió qualsevol.
- El menor complementari de l'element aij denotat per Mij és aquell element que es troba en el mig de la fila i de la columna j.
- A les matrius quadrades d'ordre 2, el menor complementari de qualsevol element és un nombre.
Adjunt d'un element
- A cada menor complementari se li pot assignar un signe, positiu si és parell i negatiu si és senar.
- S'anomena de l'element aij (anomenat Aij), el seu menor complementari multiplicat per (-1)i+j:
- (-1)i+jMij
Determinant d'una matriu quadrada de qualsevol ordre
- Si An = (ai+j) és una matriu quadrada d'ordren, el seu determinant s'obté per mitjà de la suma:
- |A| = a11A11 + a12A12+a13 + ··· + a1nA1n
- A = Andjunt de l'element, a = element.
- |A| = a11A11 + a12A12+a13 + ··· + a1nA1n
Propietats dels determinants
Característiques dels elements d'una columna o fila
- det(C1,C2,C3) + det(C1,C'2,C3) = det(C1,C2 + C'2,C3)
- Si una fila o columna d'una matriu quadrada es multiplica per un nombre real, el determinat de la matriu queda multiplicat per aquest nombre.
- det(C1,C2,KC3) = kdet(C1,C2,C3)
Combinacions lineals
- Si tots els elemntes d'una columna o fila d'una matriu quadrada són nuls, el determinant de la matriu és zero.
- det(C1,0,3) = det(1,Csub>2-Csub>2) = det(C1,C2,C3) - det(C1,C2,C3) = 0
- Si una matriu quadrada té dies columnes o files iguals, el seu determinant és nul.
- Si una matriu quadrada, una columna o fila és proporcional a una altra, el seu determinant és nul.
- det(C1,λC2,C3) = λdet(C1,C2,C3) = 0
- Si en una matriu quadrada una columna o fila és combinació de les seves paral·leles, el seu determinant és nul.
Transformacions en les matrius
- Si en una matriu quadrada s'intercanvien entre elles dues columnes o dues files, el seu determinant canvia de signe.
- Si en una matriu quadrada se suma a una columna o una fila una combinació lineal de les seves paral·leles, el determinant no varia.
- Si es transposa una matriu quadrada, el seu determinant no varia: |A|=|At|.
Operacions amb matrius
- det(A·B) = det(A) · det(B)
- , que aquesta relació s'obté de:
Determinant d'una matriu triangular
- El determinant d'una matriu triangular és igual al producte dels elements de la diagonal principal.
Càlcul de determinants pel mètode de Gauss
- Es tracta que a partir de transformacions senzilles (tenint en compte que s'està calculant el determinant) aconseguir transformar la matriu en una matriu triangular.
Calcular el rang a partir dels menors d'una matriu
- Es tracta d'agafar els menors (de dimensió més petita a més gran) i fer el càlcul d'ells. En el cas que el determinant del menor sigui diferent de 0 s'entendrà que l'ordre (n) d'aquell menor serà el rang de la matriu, sempre que no hi hagi un menor d'ordre més gran que el seu determinant sigui diferent de 0.
Calcular la matriu inversa a partir de Determinants
- Si una matriu quadrada, amb determinant diferent de 0 ( det(A) ≠ 0 ), amb aquesta fórmula pot calcular la matriu inversa:
Equacions Matricials
Regla de la suma
- Si se suma la mateixa matriu als dos membres d'una igualtat matricial, es manté la igualtat.
Regla del producte
- Si es multipliquen els dos membres d'una igualtat per un nombre real, es manté la igualtat.
- Si es multipliquen els dos membres d'una equació matricial per una matriu, com que el producte de matriu no és commutatiu cal tenir en compte el costat pel qual es multiplica:
- Si es multipliquen per l'esquerra els dos membres d'una igualtat matricial per una matriu, es manté la igualtat i el mateix si es multipliquen a la dreta els dos membres de la igualtat matricial, però mai un a l'esquerra i un a la dreta.
Extracció de factor comú
- Les propietats associatives permeten treure factor comú en una expressió matricial sempre que el factor es repeteixi al mateix costat de cada producte.
Representació dels punts anteriors
- Llavors tenien en compte tot el dit i que:
- Podem dir que:
- I en cas que no es pugui aplicar els casos anteriors, el que podem fer és substituir X per una matriu amb lletres: