Introducció als grafs: diferència entre les revisions
De FFAWiki
| (Hi ha 2 revisions intermèdies del mateix usuari que no es mostren) | |||
| Línia 41: | Línia 41: | ||
===Isomorfisme de grafs=== | ===Isomorfisme de grafs=== | ||
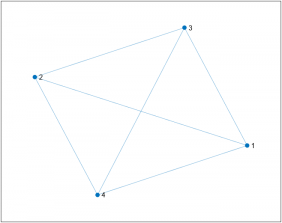
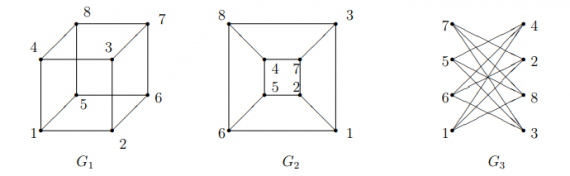
:* Dos grafs són isomorfs si canviant els noms d'un dels grafs els dos es poden representar de la mateixa manera tenint els mateixos vèrtex i arestes. | |||
::[[Fitxer:ExempleGrafIsomorfisme.png|570x570px]] | |||
===Operacions amb grafs=== | ===Operacions amb grafs=== | ||
===La seqüència de graus d’un graf=== | ===La seqüència de graus d’un graf=== | ||
Revisió de 11:08, 21 maig 2023
Grafs
Definicions
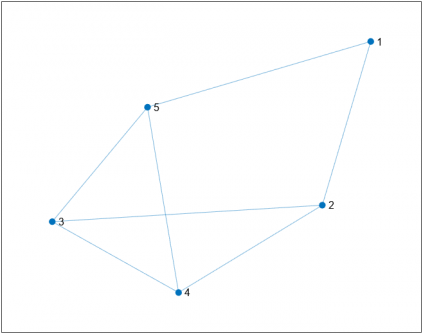
- Un Graf G(V,A) esta format per vèrtexs (V) i les connexions entre vèrtexs, les arestes (A).
- V = {1, 2, 3, 4, 5}
- A = {{1, 2}, {5, 1}, {5, 4}, {4, 2}, {3, 4}, {3, 5}, {2, 3}}
- Un graf com a tal no te multiplicitat d'arestes ni vèrtexs que connecten amb si mateix.
- Els graf amb multiplicitat d'arestes s'anomenen Multigrafs.
- Les arestes que connecten un vèrtex amb si mateix s'anomenen llaços i el graf passa a anomenar-se pseudograf.
- Un Graf G(V,A) esta format per vèrtexs (V) i les connexions entre vèrtexs, les arestes (A).
Propietats
- El nombre d'arestes d'un graf:
- n*(n-1)/2
- El nombre d'arestes d'un pseudograf:
- n*(n+1)/2
- Lema de les encaixades:
- La suma de tots els graus dels vèrtexs d'un graf o pseudograf és igual a dues vegades el nombre d'arestes.
- El nombre de vèrtexs de grau senar d'un graf és parell.
- El nombre d'arestes d'un graf:
Tipus especials de grafs
- Graf nul. Nn On n es mes petit o igual a 1. Te n vèrtex i 0 arestes.
- N4
- Graf r-regular. Tots els vèrtex amb el mateix grau r
- 3-regular
- Graf complet. Kn on n es mes gran o igual a 2. Te n vèrtexs i totes les aretes possibles.
- K 3
- Graf cicle. Cn on n es mes gran o igual a 3 cada vèrtex esta connectat per dos arestes formant un cicle.
- C4
- Graf trajecte. Tn on n es mes gran o igual a 2 cada vèrtex està connectat per dos arestes menys l'últim i el primer que nomes en tenen una formant un trajecte
- T3
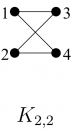
- Graf bipartit. Els vèrtex es poden separar en dos subconjunts en les que cada vèrtex d'un grup no esta connectat directament entre si.
- Graf bipartit complet. Els vèrtex es poden separar en dos subconjunts en les que cada vèrtex d'un grup no esta connectat directament entre si. Te totes les arestes que complexin la norma de l'esmentat anteriorment.
- Graf nul. Nn On n es mes petit o igual a 1. Te n vèrtex i 0 arestes.
Isomorfisme de grafs
- Dos grafs són isomorfs si canviant els noms d'un dels grafs els dos es poden representar de la mateixa manera tenint els mateixos vèrtex i arestes.