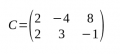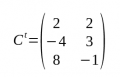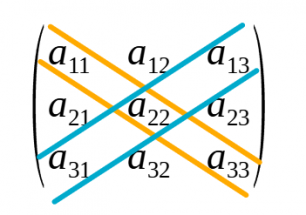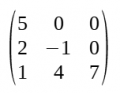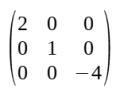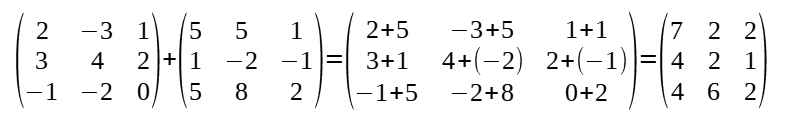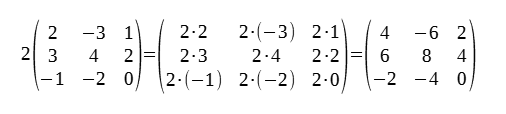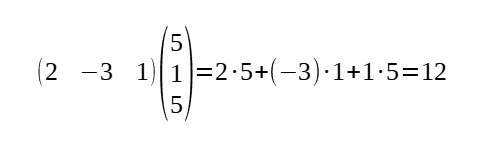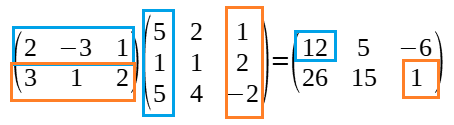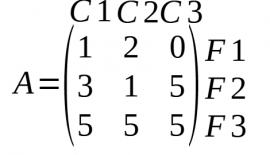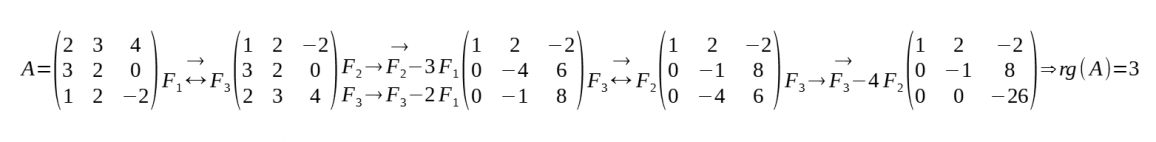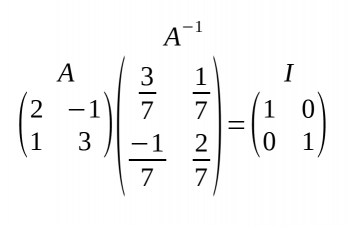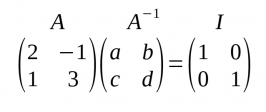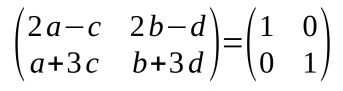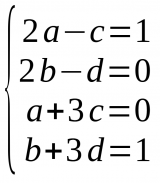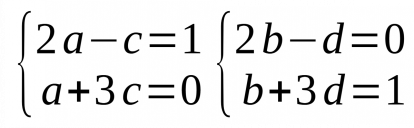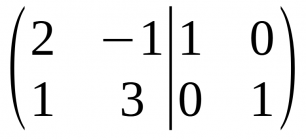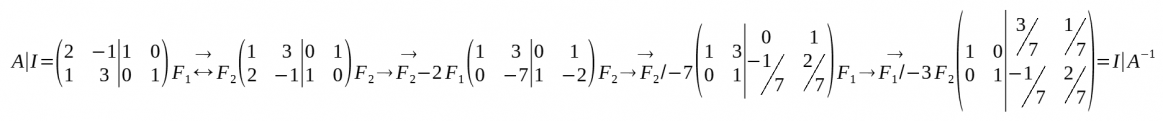Matrius: diferència entre les revisions
De FFAWiki
| (Hi ha 88 revisions intermèdies del mateix usuari que no es mostren) | |||
| Línia 30: | Línia 30: | ||
==Classificació de matrius quadrades== | ==Classificació de matrius quadrades== | ||
* Les matrius quadrades no | * Les matrius quadrades no són de dimensió m x n sinó n x n. | ||
* a<sub>ii</sub>(Són aquells elements que són a la amteixa posició de fila i de columna), a<sub>ij</sub> són els elements que la posició de fila no és la mateixa que la de la columna. | |||
*A les matrius quadrades els elements en els quals l'índex de la fila és igual al de la columna formen la '''diagonal principal''' i són de la forma a<sub>ii.</sub> | * A les matrius quadrades els elements en els quals l'índex de la fila és igual al de la columna formen la '''diagonal principal''' i són de la forma a<sub>ii.</sub> (a<sub>11</sub>, a<sub>22</sub>, a<sub>33</sub>) | ||
*Els elements de la forma a<sub>ij</sub> amb i + j = n + 1 formen la '''diagonal secundària'''. | * Els elements de la forma a<sub>ij</sub> amb i + j = n + 1 formen la '''diagonal secundària'''. | ||
[[Fitxer:Diagonals.png|none|miniatura|<nowiki>Taronja -> Diagonal principal | Blau -> diagonal secundària</nowiki>|alt=|306x306px]] | :[[Fitxer:Diagonals.png|none|miniatura|<nowiki>Taronja -> Diagonal principal | Blau -> diagonal secundària</nowiki>|alt=|306x306px]] | ||
* Una matriu quadrada s'anomena triangular superior si són nuls tots els elements situats a sota la diagonal principal i s'anomena triangular inferior si són nuls tots els elements situats a sobre la diagonal principal. | * Una matriu quadrada s'anomena '''triangular superior''' si són nuls tots els elements situats a sota la diagonal principal i s'anomena '''triangular inferior''' si són nuls tots els elements situats a sobre la diagonal principal. | ||
*La matriu identitat o unitat és una matriu escalar en la qual els elements de la diagonal principal són tots 1. Si és d'ordre n, es denota per '''I<sub>n</sub>'''. | * La '''matriu identitat o unitat''' és una matriu escalar en la qual els elements de la diagonal principal són tots 1. Si és d'ordre n, es denota per '''I<sub>n</sub>'''. | ||
* Una matriu quadrada és '''simètrica''' si es compleix que a<sub>ij</sub> = a<sub>ji</sub>, 1 ≤ i ≤ n i 1 ≤ j ≤ n. | |||
* Una matriu quadrada és '''antisimètrica''' si es compleix que a<sub>ij</sub> = -a<sub>ji</sub>, 1 ≤ i ≤ n i 1 ≤ j ≤ n. | |||
** A les matrius simètriques es compleix que A = A<sup>t</sup> i a les antisimètriques, A = -A<sup>t</sup>. | |||
<gallery> | |||
Fitxer:MatriuTriangularSuperior.png|Matriu Triangular Superior | |||
Fitxer:MatriuTriangularInferior.png|Matriu Triangular Inferior | |||
Fitxer:MatriuDiagonal.png|Matriu Diagonal | |||
Fitxer:MatriuEscalar.png|Matriu Escalar | |||
Fitxer:MatriuSimetrica.png|Matriu Simètrica | |||
Fitxer:MatriuAntisimetrica.png|Matriu Antisimètrica | |||
</gallery> | |||
==Suma de matrius== | |||
* Només es poden sumar aquelles matrius de la mateixa dimensió, se suma element per element i això crea una matriu nova. | |||
** S = A<sub>ij</sub> + B<sub>ij</sub> | |||
:[[Fitxer:ExSumaMatrius.png|none|frame|<nowiki>Exemple de suma de Matrius</nowiki>]] | |||
===Propietats de Sumes de Matrius=== | |||
* La suma de matrius té les mateixes propietats conegudes de la suma de nombres reals. | |||
* Si A<sub>mxn</sub> = (a<sub>ij</sub>), B<sub>mxn</sub> = (b<sub>ij</sub>) i C<sub>mxn</sub> = (c<sub>ij</sub>) són matrius de dimensió mxn, es compleixen les propietats: | |||
:#'''Commutativa:''' A + B = B + A | |||
:## (a + b)<sub>ij</sub> = a<sub>ij</sub> + b<sub>ij</sub> = b<sub>ij</sub> + a<sub>ij</sub> = (b + a)<sub>ij</sub> | |||
:# '''Associativa:''' (A + B) + C = A + (B + C) | |||
:## ((a + b) + c)<sub>ij</sub> = (a<sub>ij</sub> + b<sub>ij</sub>) + c<sub>ij</sub> = a<sub>ij</sub> + (b<sub>ij</sub> + c<sub>ij</sub>) = (a + (b + c))<sub>ij</sub> | |||
:# '''Element neutre:''' la matriu O<sub>mxn</sub> és l'element neutre, és a dir, A<sub>mxn</sub> + O<sub>mxn</sub> = A<sub>mxn</sub> | |||
:## (a + 0)<sub>ij</sub> = a<sub>ij</sub> + 0 = a<sub>ij</sub>. L'element ij de la matriu A<sub>mxn</sub> + 0<sub>mxn</sub> és a<sub>ij</sub> + o<sub>ij</sub> = a<sub>ij</sub> + 0 = a<sub>ij</sub> | |||
:# '''Matriu opasada:''' existeix una altre matriu, (-A)<sub>mxn</sub>, que compleix: A<sub>mxn</sub> + (-A)<sub>mxn</sub> = O<sub>mxn</sub> | |||
:## Els elements de la matriu (-A)<sub>mxn</sub> sóm els oposats als de la matriu A<sub>mxn</sub>: (-a)<sub>ij</sub> = -a<sub>ij</sub> | |||
:# '''Transposada de la suma:''' (A + B)<sup>t</sup> = A<sup>t</sup> + B<sup>t</sup> | |||
==Producte d'un nombre real per una matriu== | |||
* En multiplicar un nombre real amb una matriu crea una matriu nova. | |||
* Per multiplicar agafes el nombre real i el multipliques per cada element de la matriu. | |||
:[[Fitxer:ProducteNombreRealPerMatriu.png|none|frame|<nowiki>Exemple de multiplicació de matriu per un nombre real</nowiki>]] | |||
===Propietats del producte de nombres reals per matrius=== | |||
* Si A<sub>mxn</sub> = (a<sub>ij</sub>) i B<sub>mxn</sub> = (b<sub>ij</sub>) són matrius de dimensió mxn i , λ, μ ∈ ℝ, es compleixen les propietats: | |||
:#'''Commutativa:''' λ''A = Aλ'' | |||
:#'''Distributiva respecte a la suma de matrius:''' λ (A + B) = λA + λB | |||
:#'''Distributiva respecte la suma de nombres:''' (λ + μ)A = λA + μA | |||
:#'''Associativa:''' λ(μ''A'') ''= (λμ)A'' | |||
:#'''Producte per la unitat:''' 1''A = A'' | |||
==Producte d'una matriu fila per una matriu columna== | |||
* Es poden multiplicar si tenen el mateix nombre d'elements. | |||
* El resultat és una matriu d'un sol element. | |||
:[[Fitxer:ProducteMatriuFilaColumna.png|none|frame|<nowiki>Exemple d'una matriu fila per una matriu columna</nowiki>]] | |||
==Producte de dues matrius== | |||
* Si el nombre de columnes de la primera coincideix amb el nombre de files de la segona, es poden multiplicar. | |||
* El resultat serà una matriu amb el nombre de files de la primera i amb el nombre de columnes de la segona. | |||
* El producte de les matrius no és commutatiu. | |||
* No són aplicables les fórmules dels productes notables. | |||
* Només es pot treure factor comú quan el factor es repeteix a l'esquerra o quan es repeteix a la dreta. no es pot treure factor comú en expressions com: AB + CA. | |||
:[[Fitxer:ProducteDeDuesMatrius.png|none|frame|<nowiki>Exemple de producte de dues matrius</nowiki>]] | |||
Si A, B i C tenen la dimensió adequada per poder fer les sumes i els productes, el producte de matrius compleix les propietats següents: | |||
:#'''Associativa:''' A(BC) = (AB)C | |||
:#'''Distributiva:''' (A + B)C = AC + BC C(A + B) = CA + CB | |||
:#'''Element neutre:''' I<sub>m</sub> A<sub>mxn</sub> = A<sub>mxn</sub> A<sub>mxn</sub> I<sub>n</sub> = A<sub>mxn</sub> | |||
:#'''Transposada del producte:''' (AB)<sup>t</sup> = B<sup>t</sup>A<sup>t</sup> | |||
==Potència d'una matriu== | |||
* Per fer la potència d'una matriu (A<sup>2</sup>) s'ha de multiplicar la matriu per ella mateixa, tantes vegades com diu l'exponent. | |||
:[[Fitxer:PotenciaMatriu.png|cap|miniatura|448x448px]] | |||
==Rang d'una matriu== | |||
* El rang d'una matriu A, donat rg(A), és el nombre de files (o columnes) linealment independents. | |||
:[[Fitxer:MatriuRangFilesColumnes.png|none|alt=|miniatura|270x270px]] | |||
===Rang per files=== | |||
: En saber quantes files són independents sabem el '''rang de files'''. | |||
::F<sub>3</sub> = 2F<sub>1</sub> + F<sub>2</sub>, rang de les files és 2 | |||
===Rang per columnes=== | |||
:En saber quantes columnes són independents sabem el '''rang de columnes'''. | |||
::C<sub>2</sub> = 2C<sub>1</sub> - C<sub>3</sub>, rang de les columnes és 2 | |||
===Transformacions que conserven el rang=== | |||
* En fer les transformacions següents el rang de la matriu no canvia, per tant ens poden ajudar a treure el rang de la matriu: | |||
:# Intercanviar dues files o dues columnes de posició. | |||
:# Multiplicar els elements d'una fila o columna pel mateix nombre real diferent de zero. | |||
:# Sumar a una fila o columna una altra multiplicada per un nombre ral. | |||
:# Sumar a una fila o columna una combinació lineal de les seves paral·leles. Multiplicar una fila o una columna per un nombre diferent de zero no altera el rang; per tant, poden multiplicar-se tantes files o columnes com vulguem. Una vegada multiplicades, poden sumar-se a una d'aquestes la resta. | |||
:# Eliminar una fila o columna combinació lineal de les seves paral·leles. Com que és combinació lineal de files o columnes paral·leles, no contribueix al nombre de files o columnes linealment independents. | |||
:# Eliminar una fila o columna proporcional a una altra, ja que com que és proporcional, és combinació lineal d'aquesta. | |||
:# Eliminar una fila o columna de zeros, ja que una fila o columna de zeros és sempre igual a una altra multiplicada per zero. | |||
:# Transposar la matriu. El rang per files (o per columnes) passa a ser el rang per columnes (o per files), i viceversa. | |||
===Càlcul del rang d'una matriu pel mètode de Gauss=== | |||
* Es tracta d'esglaonar la matriu per files: | |||
:* Una matriu esglaonada per files és aquella en la que el primer element no nul de cada fila és més a la dreta al de la fila anterior i les files nul·les estan situades a la part inferior. | |||
::# Es realitzen successives [[#Transformacions que conserven el rang | transformacions]] elementals per files de la matriu fins a aconseguir una matriu equivalent esglaonada per files. | |||
::# El rang és el nombre de files no nul·les de la matriu per files. | |||
:[[Fitxer:RangMatriuGaussJordan.png|miniatura|1156x1156px|alt=|cap]] | |||
==Matriu inversa== | |||
* Una matriu quadrada és regular o invertible si existeix una altra matriu B, d'igual dimensió. | |||
* Una matriu quadrada pot no tenir inversa i aquestes s'anomenen matriu singulars. | |||
===Regeles a complir perquè la matriu tingui inversa (Propietats d'una matriu)=== | |||
* Ha de ser quadrada (files = columnes). | |||
* El Rang ha de ser igual a l'ordre de la matriu (rg(A)=n). | |||
* (A·B)<sup>-1</sup> = B<sup>-1</sup> · A<sup>-1</sup> | |||
* (A<sup>-1</sup>)<sup>-1</sup> = A | |||
* (A·B)<sup>t</sup> = B<sup>t</sup> · A<sup>t</sup> | |||
* (A<sup>t</sup>)<sup>t</sup> = A | |||
* A · A<sup>-1</sup> = A<sup>-1</sup>· A = I | |||
* AB = I → B = A<sup>-1</sup> | A = B<sup>-1</sup> | |||
:[[Fitxer:CalculInversaMatriu.png|cap|miniatura|350x350px|<nowiki>A = Matriu | A</nowiki><sup>-1</sup><nowiki> = Matriu inversa | I = Matriu identitat</nowiki>]] | |||
===Càlcul de la matriu inversa=== | |||
# Apliquem la propietat A · A<sup>-1</sup> = I, posant lletres on hauria d'haver-hi la matriu inversa:[[Fitxer:Pas1CaluclanMatriuInversa.png|alt=|cap|miniatura|266x266px]] | |||
# Multipliquem A per A<sup>-1</sup>:[[Fitxer:Pas2CaluclanMatriuInversa.png|cap|miniatura|343x343px]] | |||
# Creem un sistema d'equacions igualant cada element de la matriu amb esquerra (la que té lletres) per cada element de la matriu de la dreta (la matriu identitat):[[Fitxer:Pas3CaluclanMatriuInversa.png|cap|miniatura|183x183px]] | |||
# Creem en aquest cas dos sistemes d'equacions amb les combinacions més bones per resoldre les dues incògnites:[[Fitxer:Pas4CaluclanMatriuInversa.png|cap|miniatura|414x414px]] | |||
# Escollim el mètode de resolució dels sistemes ('''Substitució, Reducció o Igualació''') i substituïm en la matriu A<sup>-1</sup> pels valors donats en els sistemes d'equacions[[Fitxer:CalculInversaMatriu.png|cap|miniatura|350x350px|<nowiki>A = Matriu | A</nowiki><sup>-1</sup><nowiki> = Matriu inversa | I = Matriu identitat</nowiki>]] | |||
===Càlcul de la matriu inversa pel mètode de Gauss-Jordan=== | |||
* Es tracta de crear una nova matriu identitat de les mateixes dimensions que les matrius quadrades i posar-les una al costat de l'altre separades per un |, ( A | I ). | |||
:[[Fitxer:Pas1GaussJordan.png|cap|miniatura|306x306px|<nowiki>( A | I )</nowiki>]] | |||
* Un cop fet el pas anterior, has d'intentar a partir de[[#Transformacions que conserven el rang | transformacions]] passar la matriu identitat a l'altre costat del |, quedant així on estava la matriu identitat la inversa, ( I |A<sup>-1</sup> ). | |||
:[[Fitxer:Pas2GaussJordan.png|cap|miniatura|1163x1163px]] | |||
Revisió de 09:42, 10 gen 2022
Definició
- Una matriu és un conjunt d'elements organitzats en files i columnes, i cada element és una dada.
Dimensions de matrius
- Les dimensions de les matrius es mesuren per m × n, on m són les files i n les columnes.
Matrius iguals
- Dues matrius són iguals si són de la mateixa dimensió i els elements que ocupen la mateixa posició en les dues són iguals.
Matrius Transposades
- Quan s'intercanvia files per columnes s'obté la seva transposada.
Classificació de Matrius
Classificació de matrius quadrades
- Les matrius quadrades no són de dimensió m x n sinó n x n.
- aii(Són aquells elements que són a la amteixa posició de fila i de columna), aij són els elements que la posició de fila no és la mateixa que la de la columna.
- A les matrius quadrades els elements en els quals l'índex de la fila és igual al de la columna formen la diagonal principal i són de la forma aii. (a11, a22, a33)
- Els elements de la forma aij amb i + j = n + 1 formen la diagonal secundària.
- Una matriu quadrada s'anomena triangular superior si són nuls tots els elements situats a sota la diagonal principal i s'anomena triangular inferior si són nuls tots els elements situats a sobre la diagonal principal.
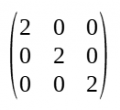
- La matriu identitat o unitat és una matriu escalar en la qual els elements de la diagonal principal són tots 1. Si és d'ordre n, es denota per In.
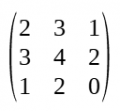
- Una matriu quadrada és simètrica si es compleix que aij = aji, 1 ≤ i ≤ n i 1 ≤ j ≤ n.
- Una matriu quadrada és antisimètrica si es compleix que aij = -aji, 1 ≤ i ≤ n i 1 ≤ j ≤ n.
- A les matrius simètriques es compleix que A = At i a les antisimètriques, A = -At.
Suma de matrius
- Només es poden sumar aquelles matrius de la mateixa dimensió, se suma element per element i això crea una matriu nova.
- S = Aij + Bij
Propietats de Sumes de Matrius
- La suma de matrius té les mateixes propietats conegudes de la suma de nombres reals.
- Si Amxn = (aij), Bmxn = (bij) i Cmxn = (cij) són matrius de dimensió mxn, es compleixen les propietats:
- Commutativa: A + B = B + A
- (a + b)ij = aij + bij = bij + aij = (b + a)ij
- Associativa: (A + B) + C = A + (B + C)
- ((a + b) + c)ij = (aij + bij) + cij = aij + (bij + cij) = (a + (b + c))ij
- Element neutre: la matriu Omxn és l'element neutre, és a dir, Amxn + Omxn = Amxn
- (a + 0)ij = aij + 0 = aij. L'element ij de la matriu Amxn + 0mxn és aij + oij = aij + 0 = aij
- Matriu opasada: existeix una altre matriu, (-A)mxn, que compleix: Amxn + (-A)mxn = Omxn
- Els elements de la matriu (-A)mxn sóm els oposats als de la matriu Amxn: (-a)ij = -aij
- Transposada de la suma: (A + B)t = At + Bt
- Commutativa: A + B = B + A
Producte d'un nombre real per una matriu
- En multiplicar un nombre real amb una matriu crea una matriu nova.
- Per multiplicar agafes el nombre real i el multipliques per cada element de la matriu.
Propietats del producte de nombres reals per matrius
- Si Amxn = (aij) i Bmxn = (bij) són matrius de dimensió mxn i , λ, μ ∈ ℝ, es compleixen les propietats:
- Commutativa: λA = Aλ
- Distributiva respecte a la suma de matrius: λ (A + B) = λA + λB
- Distributiva respecte la suma de nombres: (λ + μ)A = λA + μA
- Associativa: λ(μA) = (λμ)A
- Producte per la unitat: 1A = A
Producte d'una matriu fila per una matriu columna
- Es poden multiplicar si tenen el mateix nombre d'elements.
- El resultat és una matriu d'un sol element.
Producte de dues matrius
- Si el nombre de columnes de la primera coincideix amb el nombre de files de la segona, es poden multiplicar.
- El resultat serà una matriu amb el nombre de files de la primera i amb el nombre de columnes de la segona.
- El producte de les matrius no és commutatiu.
- No són aplicables les fórmules dels productes notables.
- Només es pot treure factor comú quan el factor es repeteix a l'esquerra o quan es repeteix a la dreta. no es pot treure factor comú en expressions com: AB + CA.
Si A, B i C tenen la dimensió adequada per poder fer les sumes i els productes, el producte de matrius compleix les propietats següents:
- Associativa: A(BC) = (AB)C
- Distributiva: (A + B)C = AC + BC C(A + B) = CA + CB
- Element neutre: Im Amxn = Amxn Amxn In = Amxn
- Transposada del producte: (AB)t = BtAt
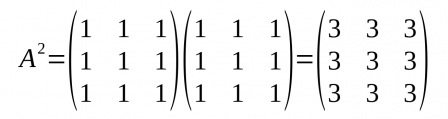
Potència d'una matriu
- Per fer la potència d'una matriu (A2) s'ha de multiplicar la matriu per ella mateixa, tantes vegades com diu l'exponent.
Rang d'una matriu
- El rang d'una matriu A, donat rg(A), és el nombre de files (o columnes) linealment independents.
Rang per files
- En saber quantes files són independents sabem el rang de files.
- F3 = 2F1 + F2, rang de les files és 2
Rang per columnes
- En saber quantes columnes són independents sabem el rang de columnes.
- C2 = 2C1 - C3, rang de les columnes és 2
Transformacions que conserven el rang
- En fer les transformacions següents el rang de la matriu no canvia, per tant ens poden ajudar a treure el rang de la matriu:
- Intercanviar dues files o dues columnes de posició.
- Multiplicar els elements d'una fila o columna pel mateix nombre real diferent de zero.
- Sumar a una fila o columna una altra multiplicada per un nombre ral.
- Sumar a una fila o columna una combinació lineal de les seves paral·leles. Multiplicar una fila o una columna per un nombre diferent de zero no altera el rang; per tant, poden multiplicar-se tantes files o columnes com vulguem. Una vegada multiplicades, poden sumar-se a una d'aquestes la resta.
- Eliminar una fila o columna combinació lineal de les seves paral·leles. Com que és combinació lineal de files o columnes paral·leles, no contribueix al nombre de files o columnes linealment independents.
- Eliminar una fila o columna proporcional a una altra, ja que com que és proporcional, és combinació lineal d'aquesta.
- Eliminar una fila o columna de zeros, ja que una fila o columna de zeros és sempre igual a una altra multiplicada per zero.
- Transposar la matriu. El rang per files (o per columnes) passa a ser el rang per columnes (o per files), i viceversa.
Càlcul del rang d'una matriu pel mètode de Gauss
- Es tracta d'esglaonar la matriu per files:
- Una matriu esglaonada per files és aquella en la que el primer element no nul de cada fila és més a la dreta al de la fila anterior i les files nul·les estan situades a la part inferior.
- Es realitzen successives transformacions elementals per files de la matriu fins a aconseguir una matriu equivalent esglaonada per files.
- El rang és el nombre de files no nul·les de la matriu per files.
Matriu inversa
- Una matriu quadrada és regular o invertible si existeix una altra matriu B, d'igual dimensió.
- Una matriu quadrada pot no tenir inversa i aquestes s'anomenen matriu singulars.
Regeles a complir perquè la matriu tingui inversa (Propietats d'una matriu)
- Ha de ser quadrada (files = columnes).
- El Rang ha de ser igual a l'ordre de la matriu (rg(A)=n).
- (A·B)-1 = B-1 · A-1
- (A-1)-1 = A
- (A·B)t = Bt · At
- (At)t = A
- A · A-1 = A-1· A = I
- AB = I → B = A-1 | A = B-1
Càlcul de la matriu inversa
- Apliquem la propietat A · A-1 = I, posant lletres on hauria d'haver-hi la matriu inversa:
- Multipliquem A per A-1:
- Creem un sistema d'equacions igualant cada element de la matriu amb esquerra (la que té lletres) per cada element de la matriu de la dreta (la matriu identitat):
- Creem en aquest cas dos sistemes d'equacions amb les combinacions més bones per resoldre les dues incògnites:
- Escollim el mètode de resolució dels sistemes (Substitució, Reducció o Igualació) i substituïm en la matriu A-1 pels valors donats en els sistemes d'equacions
Càlcul de la matriu inversa pel mètode de Gauss-Jordan
- Es tracta de crear una nova matriu identitat de les mateixes dimensions que les matrius quadrades i posar-les una al costat de l'altre separades per un |, ( A | I ).
- Un cop fet el pas anterior, has d'intentar a partir de transformacions passar la matriu identitat a l'altre costat del |, quedant així on estava la matriu identitat la inversa, ( I |A-1 ).