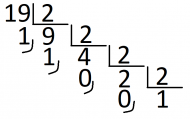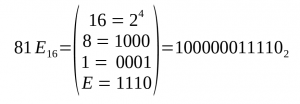Representació dels nombres: diferència entre les revisions
De FFAWiki
| Línia 73: | Línia 73: | ||
=== Representació dels nombres racionals (ℚ) === | === Representació dels nombres racionals (ℚ) === | ||
=== Representació dels nombres reals ( | === Representació dels nombres reals (ℝ) === | ||
Revisió de 13:40, 14 set 2022
Tipus de base
- Base 2 (Binari) ⇒ b = 2 ⇒ [0,1]
- Base 8 (Octal) ⇒ b = 8 ⇒ [0,1,2,3,4,5,6,7]
- Base 10 (Decimal) ⇒ b = 10 ⇒ [0,1,2,3,4,5,6,7,8,9]
- Base 16 (Hexadecimal) ⇒ b = 16 ⇒ [0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F]
Representació dels nombres naturals (ℕ)
- Per passar de Base b a Base 10 calculem les potències de polinomi equivalent
- N10 = 1405 = 1000 + 400 + 5 = 1x103 + 4 x102+ 0 x101+ 5 x100
- Per passar de Base 10 a Base b fem divisions
- Per passar de Base b1 a Base b2 passem a Base 10 i després a Base b2 (b1 ⇒ Base10 ⇒ b2)
- Ex...
- Per passar de Base b a Base bk (b1 ha de ser potència de b2) passem individualment cada número i els concatenem.
Representació dels nombres enters (ℤ)
- Per poder representar un nombre enter s'ha de saber la precisió de bits.
Signe-Magnitud
El rang de valors que podem representar és [ -(2n-1-1) , 2n-1-1 ] on n = precisió.
- El primer bit correspon al signe.
- 0 ⇒ positiu (+)
- 1 ⇒ negatiu (-)
- La resta (n-1 bits) representen el valor.
Ex...
Complement a 2
El rang de valors que podem representar és [ -(2n-1) , 2n-1-1 ] on n = precisió.
Base 10 a Base 2
- Positiu
- Passar el número a binari.
- Negatiu
- Ignorar el signe.
- Passar el número a binari.
- Fer complement a 1, és a dir canviar els 0 per 1 i els 1 per 0.
- Fer complement a 2, és a dir sumar 1 al últim bit.
Base 2 a Base 10
- Passar el número a binari.
- Mirar si esta dins el rang
- Si esta dins el rang, és positiu
- Si no esta dins el rang, és negatiu
- Fer complement a 1, és a dir canviar els 1 per 0 i els 0 per 1.
- Fer complement a 2, és a dir sumar 1 al últim bit.
(Si el primer bit és un 1 és negatiu)
Ex...
Excés a Z
El rang de valors que podem representar és [ -Z , Z+1 ] = [ -(2n-1+1) , 2n-1 ] on n = precisió.
Z = 2n-1-1
Base 10 a Base 2
- Sumar Z al número què volem convertir.
- Passar el numero a binari
Base 2 a Base 10
- Passar el numero a decimal
- Restar Z al número què hem convertit.
(Si el primer bit és un 1 és positiu)
Ex...