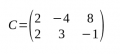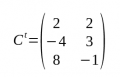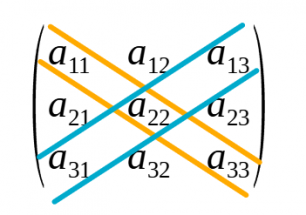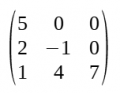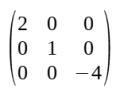Matrius

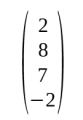
Definició

• Una matriu és un conjunt d'elements organitzats en files i columnes, i cada element és una dada.

Dimensions de matrius

• Les dimensions de les matrius es mesuren per m × n, on m són les files i n les columnes.

Matrius iguals

• Dues matrius són iguals si són de la mateixa dimensió i els elements que ocupen la mateixa posició en les dues són iguals.

Matrius Transposades

Quan s'intercanvia files per columnes s'obté la seva transposada.

• 

  Matriu C 2x3

• 

  Matriu Transposada C^t 2x3

Classificació de Matrius

• 

  Una matriu de dimensió m x n és rectangular si m ≠ n

• 

  Una matriu és quadrada si m = n

• 

  Una matriu fila és una matriu rectangular amb una sola fila

• 

  Una matriu columna és una matriu rectangular amb una sola columna

Classificació de matrius quadrades

• Les matrius quadrades no són de dimensió m x n sinó n x n.
• a_ii(Són aquells elements que són a la amteixa posició de fila i de columna), a_ij són els elements que la posició de fila no és la mateixa que la de la columna.

• A les matrius quadrades els elements en els quals l'índex de la fila és igual al de la columna formen la diagonal principal i són de la forma a_ii. (a₁₁, a₂₂, a₃₃)
• Els elements de la forma a_ij amb i + j = n + 1 formen la diagonal secundària.

Taronja -> Diagonal principal | Blau -> diagonal secundària

• Una matriu quadrada s'anomena triangular superior si són nuls tots els elements situats a sota la diagonal principal i s'anomena triangular inferior si són nuls tots els elements situats a sobre la diagonal principal.
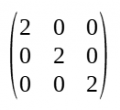
• La matriu identitat o unitat és una matriu escalar en la qual els elements de la diagonal principal són tots 1. Si és d'ordre n, es denota per I_n.
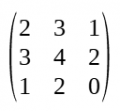
• Una matriu quadrada és simètrica si es compleix que a_ij = a_ji, 1 ≤ i ≤ n i 1 ≤ j ≤ n.
• Una matriu quadrada és antisimètrica si es compleix que a_ij = -a_ji, 1 ≤ i ≤ n i 1 ≤ j ≤ n.
  • A les matrius simètriques es compleix que A = A^t i a les antisimètriques, A = -A^t.

• 

  Matriu Triangular Superior

• 

  Matriu Triangular Inferior

• 

  Matriu Diagonal

• 

  Matriu Escalar

• 

  Matriu Simètrica

• 

  Matriu Antisimètrica

Suma de matrius

• Només es poden sumar aquelles matrius de la mateixa dimensió, se suma element per element i això crea una matriu nova.
  • S = A_ij + B_ij

Exemple de suma de Matrius