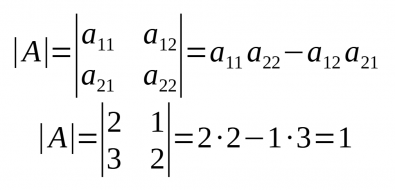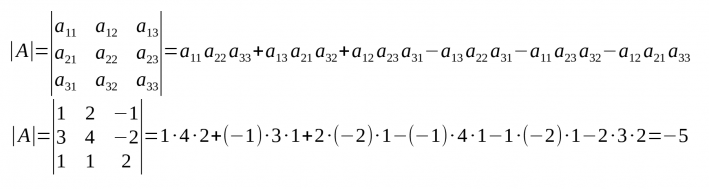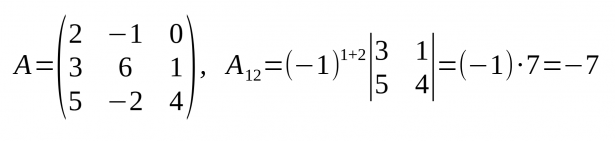Determinants: diferència entre les revisions
De FFAWiki
| Línia 27: | Línia 27: | ||
* S'anomena de l'element a<sub>ij</sub> (anomenat A<sub>ij</sub>), el seu menor complementari multiplicat per (-1)<sup>i+j</sup>: | * S'anomena de l'element a<sub>ij</sub> (anomenat A<sub>ij</sub>), el seu menor complementari multiplicat per (-1)<sup>i+j</sup>: | ||
** '''(-1)<sup>i+j</sup>M<sub>ij</sub>''' | ** '''(-1)<sup>i+j</sup>M<sub>ij</sub>''' | ||
: [[Fitxer:Adjunt.png|cap|miniatura|615x615px|És millor pensar que d'esquerra a dreta és: + - + - i així fins a acabar la matriu que fer la formula.]] | |||
Revisió del 11:51, 10 gen 2022
Definició
- A les matrius quadrades de nombres reals se'ls pot associar un nombre anomenat determinant.
Determinant d'ordre 2
- Per extreure el determinant (det(A) o |A|) d'una matriu quadrada d'ordre 2 s'ha de fer:
Determinant d'ordre 3
- Per extreure el determinant (det(A) o |A|) d'una matriu quadrada d'ordre 3 s'ha de fer:
- Per recordar els sumands del determinant d'ordre 3 i el signe podem fer servir la regla de Sarrus:.
Menor d'una matriu
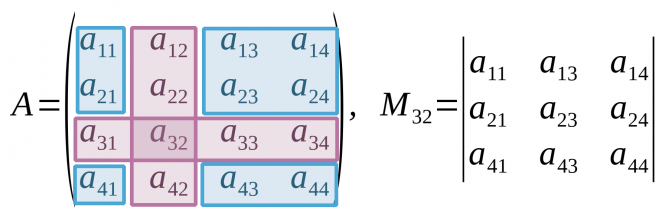
- El menor d'una matriu és aquell determinant que s'obté a partir del resultat d'eliminar d'una matriu quadrada qualsevol nombre de files o de columnes en una dimensió qualsevol.
- El menor complementari de l'element aij denotat per Mij és aquell element que es troba en el mig de la fila i de la columna j.
- A les matrius quadrades d'ordre 2, el menor complementari de qualsevol element és un nombre.
Adjunt d'un element
- A cada menor complementari se li pot assignar un signe, positiu si és parell i negatiu si és senar.
- S'anomena de l'element aij (anomenat Aij), el seu menor complementari multiplicat per (-1)i+j:
- (-1)i+jMij