Introducció als grafs: diferència entre les revisions
De FFAWiki
Cap resum de modificació |
|||
| Línia 6: | Línia 6: | ||
:**V = {1, 2, 3, 4, 5} | :**V = {1, 2, 3, 4, 5} | ||
:**A = <nowiki>{{1, 2}, {5, 1}, {5, 4}, {4, 2}, {3, 4}, {3, 5}, {2, 3}}</nowiki> | :**A = <nowiki>{{1, 2}, {5, 1}, {5, 4}, {4, 2}, {3, 4}, {3, 5}, {2, 3}}</nowiki> | ||
[[Fitxer:ExempleGraf.png|423x423px]] | ::[[Fitxer:ExempleGraf.png|423x423px]] | ||
:*Un graf com a tal no te multiplicitat d'arestes ni vèrtexs que connecten amb si mateix. | :*Un graf com a tal no te multiplicitat d'arestes ni vèrtexs que connecten amb si mateix. | ||
:*Els graf amb multiplicitat d'arestes s'anomenen '''Multigrafs'''. | :*Els graf amb multiplicitat d'arestes s'anomenen '''Multigrafs'''. | ||
| Línia 22: | Línia 22: | ||
===Tipus especials de grafs=== | ===Tipus especials de grafs=== | ||
:*'''Graf nul'''. N<sub>n</sub> On n es mes petit o igual a 1. Te n vèrtex i 0 arestes. | :*'''Graf nul'''. N<sub>n</sub> On n es mes petit o igual a 1. Te n vèrtex i 0 arestes. | ||
:**N<sub>4</sub> [[Fitxer:ExempleGrafNul.png|239x239px]] | :**N<sub>4</sub> | ||
::[[Fitxer:ExempleGrafNul.png|239x239px]] | |||
:*'''Graf r-regular'''. Tots els vèrtex amb el mateix grau r | :*'''Graf r-regular'''. Tots els vèrtex amb el mateix grau r | ||
:**3-regular [[Fitxer:ExempleGraf3regular.png|282x282px]] | :**3-regular | ||
::[[Fitxer:ExempleGraf3regular.png|282x282px]] | |||
===Isomorfisme de grafs=== | ===Isomorfisme de grafs=== | ||
Revisió del 10:39, 21 maig 2023
Grafs
Definicions
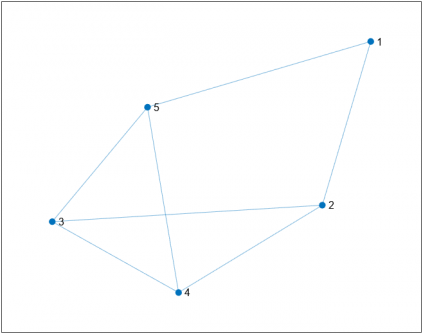
- Un Graf G(V,A) esta format per vèrtexs (V) i les connexions entre vèrtexs, les arestes (A).
- V = {1, 2, 3, 4, 5}
- A = {{1, 2}, {5, 1}, {5, 4}, {4, 2}, {3, 4}, {3, 5}, {2, 3}}
- Un graf com a tal no te multiplicitat d'arestes ni vèrtexs que connecten amb si mateix.
- Els graf amb multiplicitat d'arestes s'anomenen Multigrafs.
- Les arestes que connecten un vèrtex amb si mateix s'anomenen llaços i el graf passa a anomenar-se pseudograf.
- Un Graf G(V,A) esta format per vèrtexs (V) i les connexions entre vèrtexs, les arestes (A).
Propietats
- El nombre d'arestes d'un graf:
- n*(n-1)/2
- El nombre d'arestes d'un pseudograf:
- n*(n+1)/2
- Lema de les encaixades:
- La suma de tots els graus dels vèrtexs d'un graf o pseudograf és igual a dues vegades el nombre d'arestes.
- El nombre de vèrtexs de grau senar d'un graf és parell.
- El nombre d'arestes d'un graf:
Tipus especials de grafs
- Graf nul. Nn On n es mes petit o igual a 1. Te n vèrtex i 0 arestes.
- N4
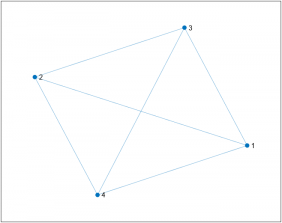
- Graf r-regular. Tots els vèrtex amb el mateix grau r
- 3-regular
- Graf nul. Nn On n es mes petit o igual a 1. Te n vèrtex i 0 arestes.