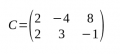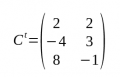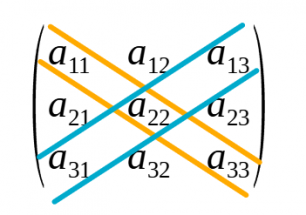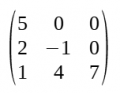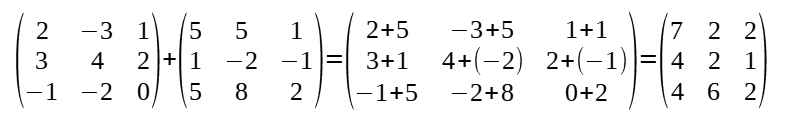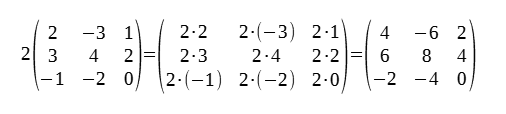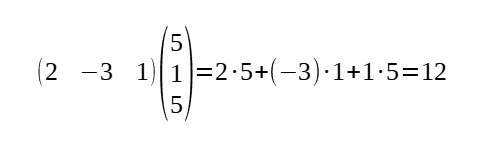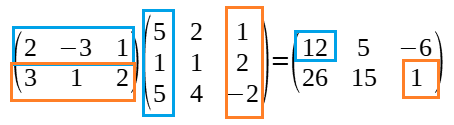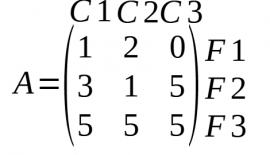Matrius
De FFAWiki
Definició
- Una matriu és un conjunt d'elements organitzats en files i columnes, i cada element és una dada.
Dimensions de matrius
- Les dimensions de les matrius es mesuren per m × n, on m són les files i n les columnes.
Matrius iguals
- Dues matrius són iguals si són de la mateixa dimensió i els elements que ocupen la mateixa posició en les dues són iguals.
Matrius Transposades
- Quan s'intercanvia files per columnes s'obté la seva transposada.
Classificació de Matrius
Classificació de matrius quadrades
- Les matrius quadrades no són de dimensió m x n sinó n x n.
- aii(Són aquells elements que són a la amteixa posició de fila i de columna), aij són els elements que la posició de fila no és la mateixa que la de la columna.
- A les matrius quadrades els elements en els quals l'índex de la fila és igual al de la columna formen la diagonal principal i són de la forma aii. (a11, a22, a33)
- Els elements de la forma aij amb i + j = n + 1 formen la diagonal secundària.
- Una matriu quadrada s'anomena triangular superior si són nuls tots els elements situats a sota la diagonal principal i s'anomena triangular inferior si són nuls tots els elements situats a sobre la diagonal principal.
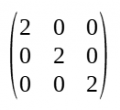
- La matriu identitat o unitat és una matriu escalar en la qual els elements de la diagonal principal són tots 1. Si és d'ordre n, es denota per In.
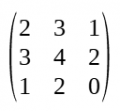
- Una matriu quadrada és simètrica si es compleix que aij = aji, 1 ≤ i ≤ n i 1 ≤ j ≤ n.
- Una matriu quadrada és antisimètrica si es compleix que aij = -aji, 1 ≤ i ≤ n i 1 ≤ j ≤ n.
- A les matrius simètriques es compleix que A = At i a les antisimètriques, A = -At.
Suma de matrius
- Només es poden sumar aquelles matrius de la mateixa dimensió, se suma element per element i això crea una matriu nova.
- S = Aij + Bij
Propietats de Sumes de Matrius
- La suma de matrius té les mateixes propietats conegudes de la suma de nombres reals.
- Si Amxn = (aij), Bmxn = (bij) i Cmxn = (cij) són matrius de dimensió mxn, es compleixen les propietats:
- Commutativa: A + B = B + A
- (a + b)ij = aij + bij = bij + aij = (b + a)ij
- Associativa: (A + B) + C = A + (B + C)
- ((a + b) + c)ij = (aij + bij) + cij = aij + (bij + cij) = (a + (b + c))ij
- Element neutre: la matriu Omxn és l'element neutre, és a dir, Amxn + Omxn = Amxn
- (a + 0)ij = aij + 0 = aij. L'element ij de la matriu Amxn + 0mxn és aij + oij = aij + 0 = aij
- Matriu opasada: existeix una altre matriu, (-A)mxn, que compleix: Amxn + (-A)mxn = Omxn
- Els elements de la matriu (-A)mxn sóm els oposats als de la matriu Amxn: (-a)ij = -aij
- Transposada de la suma: (A + B)t = At + Bt
- Commutativa: A + B = B + A
Producte d'un nombre real per una matriu
- En multiplicar un nombre real amb una matriu crea una matriu nova.
- Per multiplicar agafes el nombre real i el multipliques per cada element de la matriu.
Propietats del producte de nombres reals per matrius
- Si Amxn = (aij) i Bmxn = (bij) són matrius de dimensió mxn i , λ, μ ∈ ℝ, es compleixen les propietats:
- Commutativa: λA = Aλ
- Distributiva respecte a la suma de matrius: λ (A + B) = λA + λB
- Distributiva respecte la suma de nombres: (λ + μ)A = λA + μA
- Associativa: λ(μA) = (λμ)A
- Producte per la unitat: 1A = A
Producte d'una matriu fila per una matriu columna
- Es poden multiplicar si tenen el mateix nombre d'elements.
- El resultat és una matriu d'un sol element.
Producte de dues matrius
- Si el nombre de columnes de la primera coincideix amb el nombre de files de la segona, es poden multiplicar.
- El resultat serà una matriu amb el nombre de files de la primera i amb el nombre de columnes de la segona.
- El producte de les matrius no és commutatiu.
- No són aplicables les fórmules dels productes notables.
- Només es pot treure factor comú quan el factor es repeteix a l'esquerra o quan es repeteix a la dreta. no es pot treure factor comú en expressions com: AB + CA.
Si A, B i C tenen la dimensió adequada per poder fer les sumes i els productes, el producte de matrius compleix les propietats següents:
- Associativa: A(BC) = (AB)C
- Distributiva: (A + B)C = AC + BC C(A + B) = CA + CB
- Element neutre: Im Amxn = Amxn Amxn In = Amxn
- Transposada del producte: (AB)t = BtAt
Rang d'una matriu
Rang per files
- En saber quantes files són independents sabem el rang de files.
Rang per columnes
- En saber quantes columnes són independents sabem el rang de files.