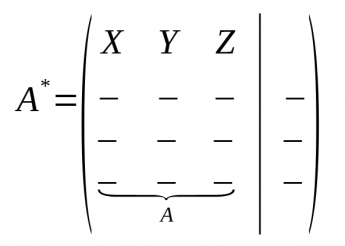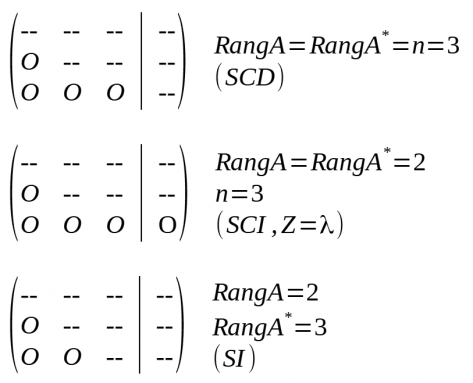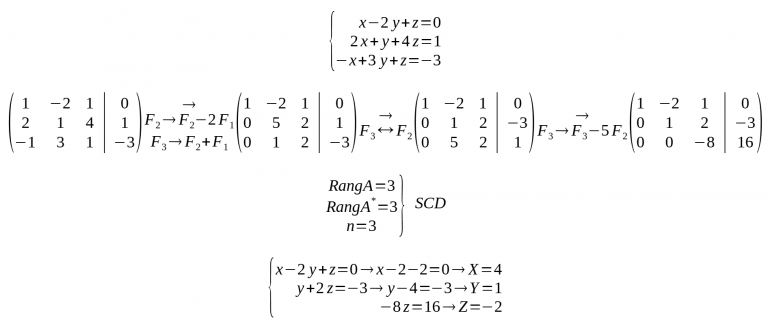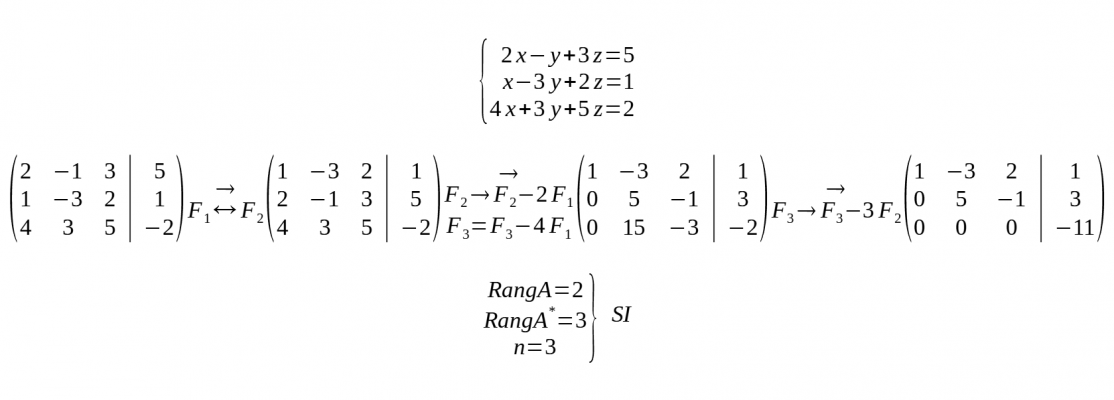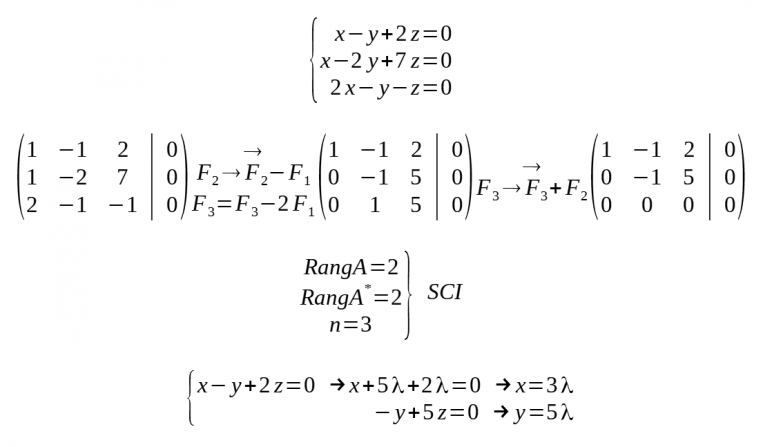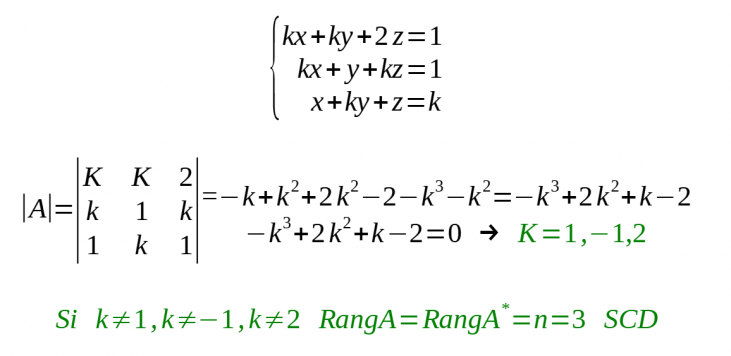Sistemes d'equacions lineals
De FFAWiki
Definició
- Un Sistema d'equacions lienals és un conjunt d'equacions que comparteixen incògnita.
Classificació
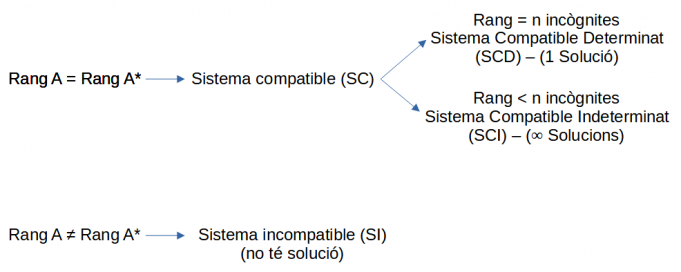
- Els sistemes es desglossen d'aquesta manera:
- I es classifiquen d'aquesta manera:
Classificació segons mètode de Gauss
Regla de Cramer
- Es pot utilitzar Cramer si:
- Té el mateix nombre d'equacions que d'incògnites.
- El determinant de la matriu dels coeficients no és nul, det(A) ≠ 0
Sistemes d'equacions resols per Gauss
- Es transforma el sistema en un altre sistema equivalent esglaonat.
- S'eliminen les equacions de la forma 0 = 0.
- Es resol el sistema esglaonat.
- Exemple SCD:
- Exemple SCI:
- Exemple SI:
Sistemes Homogenis
- Un sistema es Homogeni quan tots els seus termes independents són nuls.
- El rang de la matriu ampliada és el mateix que el de la matriu sempre posat que l'ampliada té una columna de zeros, per això tots els sistemes homogenis són compatibles.
- Aquesta solució formada per zeros s'anomena solució trivial.
- En tots els sistemes homogenis tenir solució trivial el que es busca és si tenen solucions diferents a part de la trivial.
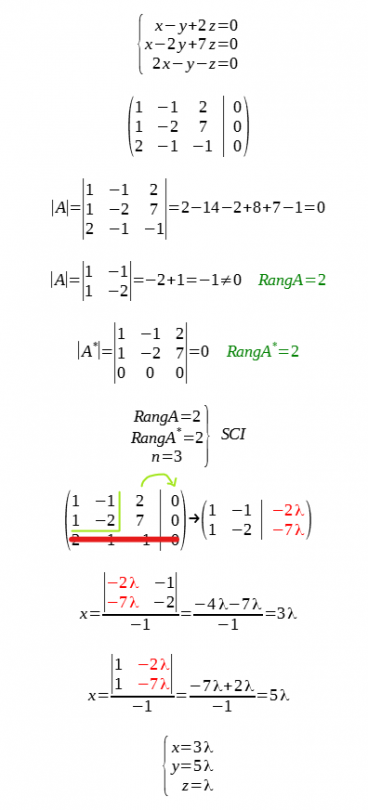
- Exemple per Cramer:
- Exemple per Gauss:
Sistemes amb paràmetres
- Calculem el rang de A per trobar quins valors de a és diferent de 0.