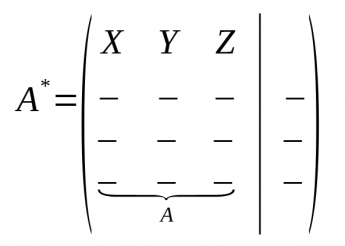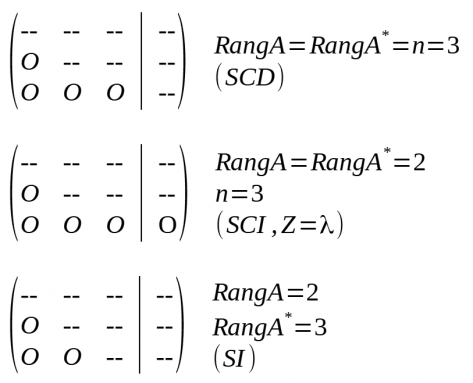Sistemes d'equacions lineals: diferència entre les revisions
De FFAWiki
| Línia 18: | Línia 18: | ||
**El determinant de la matriu dels coeficients no és nul, det(A) ≠ 0 | **El determinant de la matriu dels coeficients no és nul, det(A) ≠ 0 | ||
: [[Fitxer:ExempleCramer.png|cap|miniatura|608x608px]] | : [[Fitxer:ExempleCramer.png|cap|miniatura|608x608px]] | ||
==Sistemes d'equacions resols per Gauss== | |||
# Es transforma el sistema en un altre sistema equivalent esglaonat. | |||
# S'eliminen les equacions de la forma 0 = 0. | |||
# Es resol el sistema esglaonat. | |||
Revisió del 17:23, 22 gen 2022
Definició
- Un Sistema d'equacions lienals és un conjunt d'equacions que comparteixen incògnita.
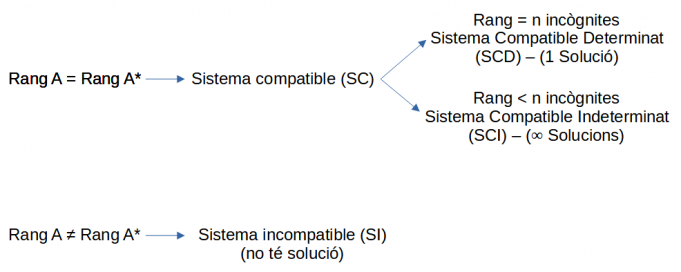
Classificació
- Els sistemes es desglossen d'aquesta manera:
- I es classifiquen d'aquesta manera:
Classificació segons mètode de Gauss
Regla de Cramer
- Es pot utilitzar Cramer si:
- Té el mateix nombre d'equacions que d'incògnites.
- El determinant de la matriu dels coeficients no és nul, det(A) ≠ 0
Sistemes d'equacions resols per Gauss
- Es transforma el sistema en un altre sistema equivalent esglaonat.
- S'eliminen les equacions de la forma 0 = 0.
- Es resol el sistema esglaonat.